Schriftliche Subtraktion

Mit Hilfe der schriftlichen Subtraktion lassen sich größere Zahlen subtrahieren. Beim schriftlichen Subtrahieren gibt es zwei verschiedene Möglichkeiten die Rechnung durchzuführen: Abziehverfahren und Ergänzungsverfahren. Beide Möglichkeiten sehen wir uns hier an. Außerdem unterscheiden wir die schriftliche Subtraktion ohne Zehnerübergang und die schriftliche Subtraktion mit Zehnerübergang (Übertrag).

Kleine Subtraktion wie 8 - 3 = 5 haben wir bereits in den Grundlagen der Subtraktion behandelt. Werden die Zahlen größer wird die schriftliche Subtraktion schwieriger. Daher setzen wir in diesem Fall die schriftliche Subtraktion ein. Diese funktioniert ähnlich wie die schriftliche Addition. Die Zahlen werden untereinander geschrieben und von hinten nach vorne Stelle für Stelle berechnet.

Zwei Verfahren sehen wir uns nun an:

• Die schriftliche Subtraktion mit Abziehverfahren.
• Die schriftliche Subtraktion mit Ergänzungsverfahren.

Ob ihr das Abziehverfahren oder das Ergänzungsverfahren für die Aufgaben nehmen möchtet, ist euch überlassen oder wird vom Lehrer oder der Lehrerin vorgegeben.

Schriftliche Subtraktion mit Abziehverfahren

Die erste Möglichkeit schriftlich zu subtrahieren ist das Abziehverfahren. Hier wird Stelle für Stelle abgezogen um das Ergebnis zu berechnen.

Beispiel 1: Abziehverfahren ohne Zehnerübergang

Berechnet werden soll 69 - 45. Wir schreiben die beiden Zahlen untereinander. Dabei steht die letzte Stelle (Einer in grün geschrieben) untereinander und die Zehnerstelle in rot steht ebenfalls untereinander. Unter einen Strich schreiben wir das Ergebnis. Seht erst einmal auf die Rechnung, die Erklärung findet ihr unterhalb.

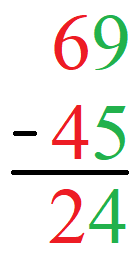
Berechnung:

• Einerstelle: 9 - 5 = 4. Wir schreiben die 4 in das Ergebnis.
• Zehnerstelle: 6 - 4 = 2. Wir schreiben die 2 in das Ergebnis.

Das Ergebnis lautet damit 24.

Beispiel 2: Abziehverfahren ohne Übertrag

Berechnet werden soll 475 - 263. Wir schreiben die Stellen für Einer (grün), die Zehner (rot) und die Hunderter (blau) untereinander. Vor die 263 kommt ein Minuszeichen. Das Ergebnis kommt unter einen Strich. Wie auch im ersten Beispiel erst die vollständige Rechnung und darunter die Erklärung.

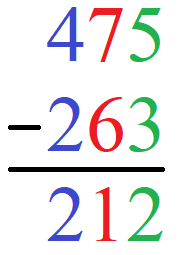
Berechnung:

• Einerstelle: 5 - 3 = 2. Wir schreiben die 2 in das Ergebnis.
• Zehnerstelle: 7 - 6 = 1. Wir schreiben die 1 in das Ergebnis.
• Hunderterstelle: 4 - 2 = 2. Wir schreiben die 2 in das Ergebnis.

Das Ergebnis lautet damit 212.

Beispiel 3: Abziehverfahren mit Zehnerübergang

Die schriftliche Subtraktion wird schwieriger wenn es einen Zehnerübergang gibt wie im nächsten Beispiel. Berechnet werden soll 426 - 258. Auch hier schreiben wir die Stellen jeweils untereinander.

Bei der Berechnung entsteht jedoch ein Übertrag, den wir im nächsten Beispiel mit einer kleinen 1 auf der Stelle davor berücksichtigen. So etwas nennt man auch einen Übertrag. Dies mag auf den ersten Blick etwas komisch aussehen. Werft dennoch erst einen Blick auf die Berechnung, unterhalb findet ihr die Erklärung.

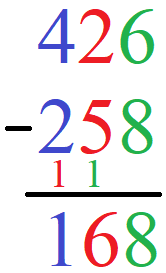
Berechnung:

• Einerstelle: 6 - 8 funktioniert nicht.
  • Daher machen wir aus der 6 eine 16. Die 1 von der 16 notieren wir auf der Zehnerstelle.
  • 16 - 8 = 8. Wir notieren die 8 im Ergebnis.
• Zehnerstelle: 2 - 5 funktioniert nicht.
  • Daher machen wir aus der 2 eine 12. Die 1 von der 12 notieren wir auf der Hunderterstelle.
  • 12 - 5 - 1 = 6. Wir notieren die 6 im Ergebnis.
• Hunderterstelle: 4 - 2 - 1 = 1.

Das Ergebnis lautet damit 168.

Schriftliche Subtraktion mit Ergänzungsverfahren

Neben dem Abziehverfahren gibt es noch das Ergänzungsverfahren um Aufgaben zur schriftlichen Subtraktion zu lösen. Starten wir mit einfachen Beispielen ohne Zehnerübergang.

Beim Ergänzungsverfahren fragt man sich was man im Ergebnis ergänzt muss damit eine Berechnung stimmt. Während beim Abziehverfahren eine Subtraktion berechnet wurde, hat man beim Ergänzungsverfahren eine Addition.

Beispiel 4: Ergänzungsverfahren ohne Zehnerübergang

Berechnet werden soll 69 - 45. Wir schreiben die Zahlen wie beim Abziehverfahren untereinander und rechnen von hinten nach vorne Stelle für Stelle.

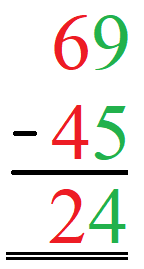
Berechnung:

• Einerstelle: 5 + ___ = 9.
  • 5 + 4 = 9.
  • Schreibe 9 in das Ergebnis.
• Zehnerstelle: 4 + ___ = 6.
  • 4 + 2 = 6
  • Schreibe 6 in das Ergebnis.

Mit dem Ergänzungsverfahren zur schriftlichen Subtraktion kommt 24 als Ergebnis raus.

Beispiel 5: Ergänzungsverfahren ohne Übertrag

Berechnet werden soll 475 - 263. Wir schreiben Einer (hier grün), Zehner (hier rot) und Hunderter (hier blau) jeweils untereinander. Im Anschluss ergänzen wir von hinten nach vorne. Zunächst wieder die Aufgabe komplett gelöst, unterhalb findet ihr die Erklärung wie die Berechnung abgelaufen ist.

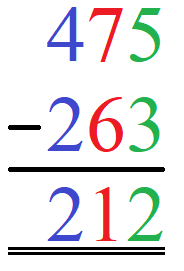
Berechnung:

• Einerstelle: 3 + ___ = 5.
  • 3 + 2 = 5.
  • Schreibe 2 in das Ergebnis.
• Zehnerstelle: 6 + ___ = 7.
  • 6 + 1 = 7
  • Schreibe 1 in das Ergebnis.
• Hunderterstelle: 2 + ___ = 4.
  • 2 + 2 = 4.
  • Schreibe 2 in das Ergebnis.

Die Differenz beträgt damit 212.

Beispiel 6: Ergänzungsverfahren mit Übertrag

Berechnet werden soll 426 - 258. Hier entsteht das Problem, dass die Stelle oben manchmal kleiner ist als die Stelle darunter. Dies führt zu einem Zehnerübergang bzw. einem Übertrag. Wie immer erst einmal die Berechnung und im Anschluss die Erklärung.

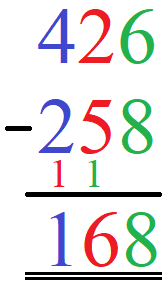
Berechnung:

• Einerstelle: 8 + ___ = 6 funktioniert so nicht.
  • Wir machen aus der 6 eine 16.
  • 8 + ___ = 16.
    • 8 + 8 = 16.
    • 8 in das Ergebnis.
    • 1 als Übertrag.
• Zehnerstelle: 5 + 1 + ____ = 2 funktioniert so nicht.
  • Wir machen aus der 2 eine 12.
  • 5 + 1 + ___ = 12.
    • 5 + 1 + 6 = 12.
    • 6 in das Ergebnis.
    • 1 als Übertag.
• Hunderterstelle: 2 + 1 + ___ = 4
  • 2 + 1 + 1 = 4.
  • 1 in das Ergebnis.

Die Differenz (Lösung der schriftlichen Subtraktion) ist damit 168.

Weiterführende Links:

• Schriftliche Subtraktion mit Komma
• Mathematik-Übersicht