Schriftliche Addition verstehen

Werden die Zahlen bei einer Addition größer, empfiehlt es sich die "schriftliche Addition" durchzuführen. Ich zeige dir hier wie man schriftlich addiert. Wir starten mit einfachen Aufgaben ohne Übertrag und gehen weiter zur schriftliche Addition mit Übertrag. Am Ende des Artikels gibt es noch eine Sachaufgabe mit Geld.

Die Addition kleinerer Zahlen lernt man bereits in der 1. Klasse. Werden die Zahlen etwas größer, verwendet man die halbschriftliche Addition oder greift - wie in diesem Artikel beschrieben - auf die schriftliche Addition zurück.

Beispiel 1: Schriftliche Addition ohne Übertrag

Berechne 23 + 74. Wie lautet das Ergebnis?

Schritt 1: Zahlen untereinander schreiben

Im ersten Schritt schreiben wir die beiden Zahlen untereinander. Wir müssen darauf achten, dass die 4 unter der 3 steht. Die 7 muss unter der 2 stehen. Damit stehen die Einerstellen (in rot) und die Zehnerstellen (in grün) untereinander.

Schritt 2: Strich ziehen

Unter die Zahlen wird ein Strich gezogen.

Schritt 3: Einerstelle berechnen

Bei der schriftlichen Addition wird von hinten nach vorne berechnet. Wir beginnen daher mit der Addition ganz hinten (bei den roten Zahlen). Hier berechnen wir 3 + 4 = 7. Die 7 schreiben wir unter den Strich.

Schritt 4: Zehnerstelle berechnen

Im Anschluss berechnen wir noch die Zehnerstelle (in grün). Wir erhalten 2 + 7 = 9. Die 9 schreiben wir ebenfalls unter den Strich.

Die Lösung dieser Aufgabe lautet nun 97. Dies bedeutet, dass 23 + 74 = 97 ist.

Schriftlich Addieren mit unterschiedlich vielen Stellen

Was passiert, wenn die Zahlen bei der schriftlichen Addition unterschiedlich viele Stellen haben? In diesem Fall muss man trotzdem darauf achten, dass die jeweils letzte Stelle (Einerstelle) untereinander steht.

Beispiel 2: Schriftliche Addition ohne Übertrag

Berechne 432 + 45. Wie lautet das Ergebnis?

Schritt 1: Zahlen untereinander schreiben

Im ersten Schritt schreiben wir die beiden Zahlen untereinander. Wir müssen darauf achten, dass die jeweils letzte Stelle der Zahlen untereinander steht. Die 5 muss daher unter der 2 stehen. Dadurch stehen die Einer (in rot) untereinander. Auch die Zehner (in grün) müssen untereinander geschrieben werden. Bei 432 steht die 4 vorne alleine, denn 45 hat keine Hunderterstelle.

Schritt 2: Strich ziehen

Unter die Zahlen wird ein Strich gezogen.

Schritt 3: Einerstelle berechnen

Bei der schriftlichen Addition wird von hinten nach vorne gerechnet. Wir beginnen daher mit der Addition ganz hinten (bei den roten Zahlen). Hier berechnen wir 2 + 5 = 7. Die 7 schreiben wir unter den Strich.

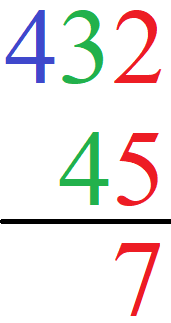
Schritt 4: Zehnerstelle berechnen

Im Anschluss berechnen wir noch die Zehnerstelle (in grün). Wir erhalten 3 + 4 = 7. Die 7 schreiben wir ebenfalls unter den Strich.

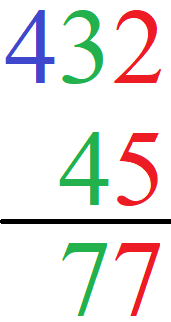
Schritt 5: Hunderterstelle berechnen

Im Anschluss berechnen wir noch die Hunderterstelle (in blau). Hier gibt es nur eine 4. Die 4 schreiben wir ebenfalls unter den Strich.

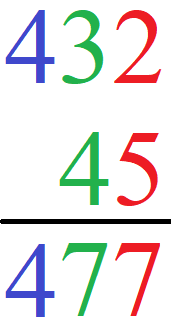
Wir erhalten 432 + 45 = 477.

Schriftliche Addition mit Übertrag

Bei der schriftlichen Addition wird Stelle für Stelle addiert. Was passiert, wenn eine Zahl dabei 10 oder größer wird? Antwort: Es entsteht ein Übertrag. Genau solch einen Übertrag sehen wir uns im nächsten Beispiel an.

Beispiel 3: Schriftliche Addition mit Übertrag

Berechne 546 + 185. Wie lautet das Ergebnis?

Schritt 1: Zahlen untereinander schreiben

Im ersten Schritt schreiben wir wieder die Zahlen untereinander: Einer unter Einer (rot), Zehner unter Zehner (grün) und Hunderter unter Hunderter (blau). Darunter ziehen wir einen Strich.

Schritt 2: Einerstelle berechnen

Wir beginnen erneut von hinten nach vorne zu rechnen. Auf der letzten Stelle haben wir 6 + 5 = 11. Die 11 besteht aus zwei Ziffern. Wie schreibt man dies nun? Die hintere 1 kommt in das Ergebnis. Die vordere 1 schreiben wir auf die Zehnerstelle, nur eben etwas kleiner. Dies nennt man einen Übertrag.

Schritt 3: Zehnerstelle berechnen

Im nächsten Schritt berechnen wir die Zehnerstelle. Wir erhalten 4 + 8 + 1 = 13. Die 1 kommt vom Übertrag der Einerstelle. Von der 13 schreiben wir die hintere Stelle (3) in das Ergebnis. Die vordere Stelle (1) übernehmen wir wieder als Übertrag auf die Stelle davor.

Schritt 4: Hunderterstelle berechnen

Fehlt uns noch die Hunderterstelle. Bei dieser erhalten wir 5 + 1 + 1 = 7. Die 7 schreiben wir in unser Ergebnis.

Die Summe aus 546 + 185 ist damit 731.

Schriftliche Addition mit Geld

Es gibt zwei Möglichkeiten die schriftliche Addition mit Geld zu behandeln. Dies umfasst erst einmal mit ganzen Euros zu rechnen. Zum Beispiel 546 Euro + 185 Euro. Alternativ können Geldbeträge auch Cents beinhalten wie zum Beispiel 546,45 Euro. Dies ist dann ein Rechnen mit Kommazahlen. Wir fangen hier mit dem einfachsten Fall an. Wer noch die schriftliche Addition mit Komma benötigt, findet diese im Anschluss mit Link

Beispiel 4: Schriftliche Addition mit Geld

Berechnet werden soll 546 Euro + 185 Euro. Wie lautet das Ergebnis?

Schritt 1: Untereinander schreiben

Wie von der schriftlichen Addition gewohnt schreiben wir die Zahlen Stellenweise untereinander. Der einzige Unterschied liegt darin, dass wir noch das Euro-Zeichen hinter die Zahlen schreiben.

Schritt 2: Ergebnis berechnen

Danach rechnen wir Stelle für Stelle von hinten nach vorne:

• 6 + 5 = 11. Die 1 in das Ergebnis, 1 als Übertrag.
• 4 + 8 + 1 = 13. Die 3 in das Ergebnis, 1 als Übertrag.
• 5 + 1 + 1 = 7. Die 7 in das Ergebnis.
• Euro-Zeichen ebenfalls in das Ergebnis schreiben.

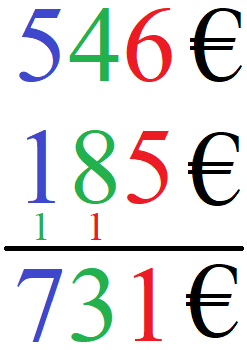
Weiterführende Inhalte:

• Schriftliche Addition mit größeren und mehr Zahlen
• Schriftliche Addition mit Komma
• Zur Mathematik-Übersicht