Brüche dividieren ▷ Erklärung und Beispiele

Brüche zu dividieren gehört zu den Grundlagen der Bruchrechnung. Wie die Division durch Multiplikation funktioniert, lernst du hier mit mit Beispielen. Zusätzlich sehen wir uns die Division mit ganzen Zahlen und gemischten Brüchen an. Die Inhalte liegen als Text und als Video vor.

Dividieren bedeutet in der Mathematik teilen oder aufteilen. Dies gilt auch beim Dividieren von Brüchen. Eine Pizza kann in 8 gleich große Stücke aufgeteilt werden. 6 der 8 Stücke wurden noch nicht gegessen und werden jetzt auf 2 Personen verteilt. Dies bedeutet 3 Stücke Pizza pro Person.

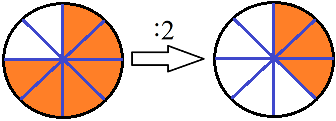
Vorgehensweise Brüche dividieren:

• Ersten Bruch unverändert lassen.
• Division durch Multiplikation ersetzen.
• Zähler und Nenner des zweiten Bruchs vertauschen.
• Zähler mit Zähler multiplizieren.
• Nenner mit Nenner multiplizieren.

Sehen wir uns dazu einige Beispiele zum Teilen von Brüchen an.

Brüche dividieren: 2 Brüche teilen

Um Brüche zu dividieren, wird die Division in eine Multiplikation verwandelt. Das Geteiltzeichen wir durch ein Malzeichen ersetzt. Um dies tun zu dürfen, wird beim zweiten Bruch Zähler und Nenner vertauscht. Im Anschluss wird wie bei der Multiplikation von Brüchen Zähler mal Zähler und Nenner mal Nenner gerechnet.

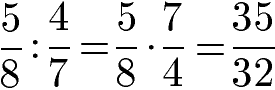
Ein weiteres Beispiel zur Division von Brüchen zeigt wie die Division durch eine Multiplikation ersetzt wird. Im Unterschied zum ersten Beispiel entsteht ein Bruch, der noch vereinfacht werden kann. So können bei 6 : 28 sowohl Zähler aus auch Nenner durch 2 geteilt werden. Zähler und Nenner durch die gleiche Zahl zu teilen wird in der Mathematik als Bruch kürzen bezeichnet.

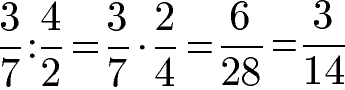
Im Gegensatz zur Addition von Brüchen oder Subtraktion von Brüchen ist es beim Dividieren von Brüchen egal, ob die Nenner der beiden Brüche gleich oder unterschiedlich sind.

Die allgemeine Schreibweise zur Division von Brüchen kann mit der folgenden Gleichung ausgedrückt werden.

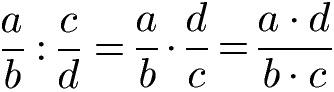
Das Vertauschen von Zähler und Nenner wird in der Mathematik Kehrwert bilden genannt. Im nächsten Abschnitt sehen wir uns gemischte Aufgaben an, bei denen in einer Aufgabe multipliziert und dividiert wird.

Brüche dividieren und multiplizieren

Die Division und Multiplikation von Brüchen kann auch in einer einzigen Aufgabe vorkommen. In der Mathematik sind Multiplikation und Division "gleich wichtig". Kommen nur Berechnungen mit gleicher Priorität vor, wird von links nach rechts gerechnet.

Im nächsten Beispiel wird zuerst die Multiplikation der beiden linken Brüche berechnet: Zähler mal Zähler und Nenner mal Nenner. Im Anschluss folgt die Division: Es wird mit dem rechten Bruch multipliziert nachdem bei diesem Zähler und Nenner vertauscht wurden.

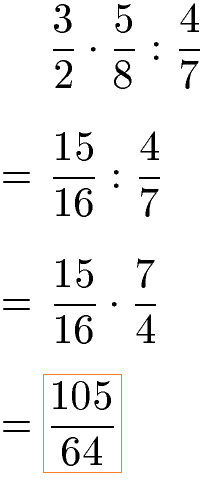
Die Reihenfolge der Berechnung von Brüchen kann durch Klammern verändert werden. In der Mathematik wird der Inhalt der Klammer zuerst berechnet. Durch Setzen von Klammern wird zuerst die Division der Brüche berechnet und danach erst die Multiplikation.

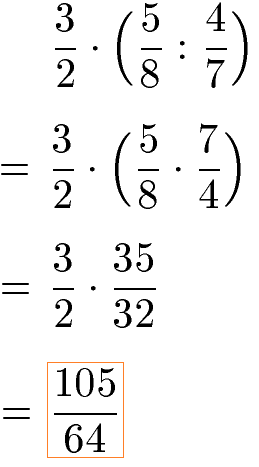
Brüche dividieren mit ganzen Zahlen und natürlichen Zahlen

Brüche können durch ganze Zahlen oder natürliche Zahlen dividiert werden. Es gibt dabei sowohl den Fall "Bruch durch Zahl" als auch "Zahl durch Bruch". Beide Möglichkeiten sehen wir uns an. Die allgemeine Schreibweise zur Berechnung von einem Bruch geteilt durch eine ganze oder natürliche Zahl sieht wie folgt aus.

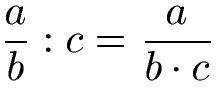
Ein einfaches Beispiel zeigt wie ein Bruch durch eine natürliche Zahl geteilt wird.

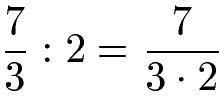
Ein Bruch kann sehr einfach durch eine ganze Zahl dividiert werden.

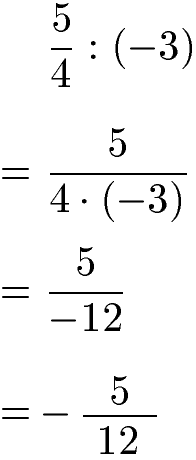
Umgekehrt kann die Möglichkeit bestehen "Zahl durch Bruch" zu berechnen. Dazu wird die ganze Zahl in einen Bruch mit Nenner 1 umgewandelt. Dadurch kann die Aufgabe wie die Division zweier Brüche behandelt werden.

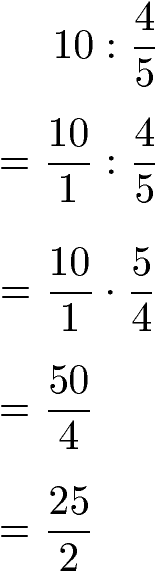
Neben ganzen Zahlen kann die Division von Brüchen auch mit gemischten Brüchen erfolgen. Sehen wir uns dazu Beispiele an.

Gemischte Zahlen oder gemischte Brüche dividieren

Gemischte Zahlen bzw. gemischte Brüche werden dividiert, indem diese zunächst in gewöhnliche Brüche mit nur Zähler und Nenner umgewandelt werden. Als Beispiel dient die Division zweier gemischter Brüche.

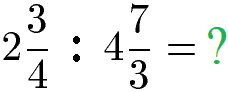
Im ersten Schritt wandeln wir die linke gemischte Zahl in einen Bruch aus nur Zähler und Nenner um. Dazu wird die ganze Zahl - in diesem Fall 2 - mit dem Nenner 4 erweitert. Mit 4 erweitern bedeutet die ganze Zahl in Zähler und Nenner mit 4 zu multiplizieren. Dadurch entstehen zwei Brüche mit gleichem Nenner, die sehr einfach addiert werden können.

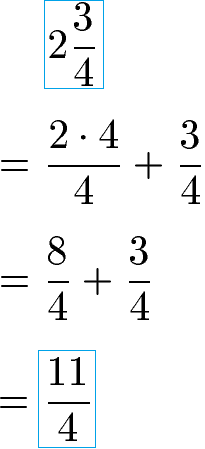
Im zwei Schritt wandeln wir die rechte gemischte Zahl in einen Bruch aus nur Zähler und Nenner um. Dazu wird die ganze Zahl - in diesem Fall 4 - mit dem Nenner 3 erweitert. Mit 3 erweitern bedeutet die ganze Zahl in Zähler und Nenner mit 3 zu multiplizieren. Dadurch entstehen zwei gleichnamige Brüche, die sehr einfach addiert werden können.

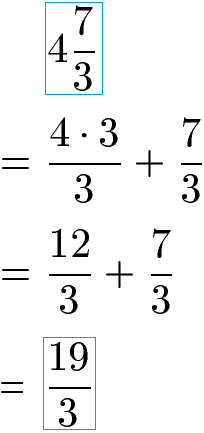
Die beiden gemischten Brüche wurden in zwei gewöhnliche Brüche mit nur Zähler und Nenner verwandelt. Diese werden im Anschluss wie eine Divisionsaufgabe zweier Brüche behandelt und berechnet.

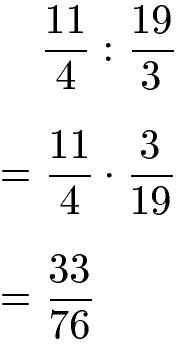
Links:

• Aufgaben / Übungen: Brüche dividieren
• Zu den Übungsaufgaben: Bruchrechnung
• Zurück zu: Bruchrechnung Übersicht
• Zurück zur Mathematik-Übersicht