Brüche kürzen ▷ Beispiele und Tricks

Brüche zu kürzen lernst du in diesem Artikel mit vielen Beispielen. Wir sehen und Tricks und Regeln an um einfache und schwierige Brüche mit Zahlen und Variablen zu kürzen. Die Inhalte liegen als Text und als Video vor.

Brüche zu kürzen bedeutet den Zähler und den Nenner eines Bruchs durch die gleiche natürliche Zahl zu teilen. Der Wert des Bruchs ändert sich dabei nicht. Der Bruch wird jedoch einfacher. Sehr einfach lässt sich dies mit einer Pizza verstehen. Sind die Stück gleich groß sind 4 von 8 Teile genau so viel wie 1 von 2 Teilen.

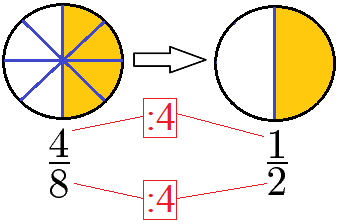
Der umgekehrte Fall besteht darin Brüche zu erweitern. Dies bedeutet den Zähler und den Nenner mit der gleichen natürlichen Zahl zu multiplizieren. Auch hier ändert sich die Größe des Bruches nicht, die gelb markierten Pizzastücke sind gleich groß.

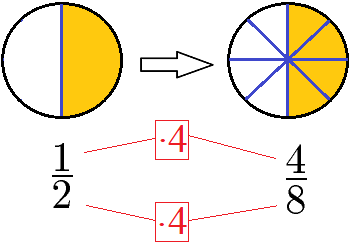
Brüche werden addiert, subtrahiert, multipliziert und dividiert. Dabei entsteht oft ein Bruch, der noch durch Kürzen vereinfacht werden kann. Sehen wir uns dazu einfache und schwierige Beispiele an.

Einfache Beispiele zum Brüche kürzen

Nicht jeder Bruch kann gekürzt werden. Manchmal lässt sich einfach keine natürliche Zahl (1, 2, 3, 4, 5, ... ) finden, durch die sich Zähler und Nenner ohne Rest teilen lassen.

Um einen Bruch zu kürzen, wird eine Kürzungszahl benötigt. In der Praxis sieht man sich die Zahlen in Zähler und Nenner an und überlegt erst einmal, ob diese durch 2 teilbar sind. Falls nein versucht man es mit der Zahl 3 und so weiter. Sehr hilfreich sind dabei die Teilbarkeitsregeln.

Beispiele Brüche kürzen

Bei der nächsten Aufgabe lassen sich Zähler und Nenner sehr einfach durch 2 teilen.

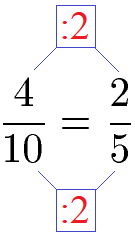
Beim nächsten Beispiel lassen sich Zähler und Nenner nicht durch 2 teilen. Jedoch sind Zähler (3) und Nenner (9) ohne Rest durch 3 teilbar. Daher kürzen wir diesen Bruch mit 3.

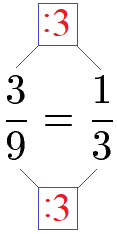
Sehr einfach ist auch das Kürzen mit der Zahl 10 falls Zähler und Nenner auf eine 0 enden.

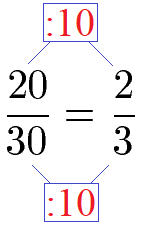
Im nächsten Abschnitt kürzen wir einmal einen größeren Bruch.

Kürzen bis zur Grunddarstellung

Brüche mit größeren Zahlen können auf verschiedene Arten gekürzt werden. Die einfachste Trick ist meistens den Bruch Schritt für Schritt zu kürzen. Versuche dabei zunächst den Bruch mit 2 oder 3 zu kürzen und danach mit einer weiteren Zahl. Sehen wir uns ein Beispiel an. Der folgende Bruch soll gekürzt werden.

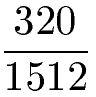
Sowohl der Zähler (320) als auch der Nenner (1512) enden auf eine gerade Zahl. Daher sind beide Zahlen ohne Rest durch 2 teilbar. Wir kürzen den Bruch daher mit 2.

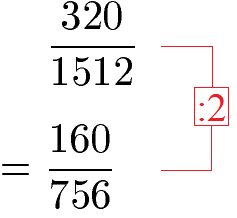
Der Bruch lässt sich jedoch noch weiter kürzen. Sowohl Zähler als auch Nenner lassen sich ohne Rest durch 4 teilen. Daher kürzen wir weiter mit der 4.

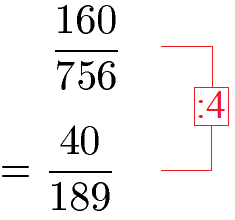
Dieser Bruch ist nun vollständig gekürzt. Vollständig gekürzt ist ein Bruch, wenn es keine natürliche Zahl (1, 2, 3, 4, ...) mehr gibt, durch die sich Zähler und Nenner ohne Rest teilen lassen. Der Bruch befindet sich nach vollständiger Kürzung in der Grunddarstellung.

Neben der Möglichkeit Schritt für Schritt zu kürzen besteht auch die Möglichkeit sofort vollständig zu kürzen. Um dies jedoch zu schaffen muss sofort durch den größten gemeinsamen Teiler (ggT) geteilt werden. Möchtest du das ggT von zwei Zahlen (Zähler und Nenner) auf diesem Weg berechnen lernst du dies unter größter gemeinsamer Teiler oder Primfaktorzerlegung.

Regeln und Tricks zum Kürzen

Wichtige Regeln zum Kürzen von Brüchen lauten:

1. Kürze einen Bruch mit einer natürlichen Zahl, aber nicht mit 0.
2. Der Wert des Bruchs darf sich beim Kürzen nicht ändern.
3. Aus Differenzen und Summen kürzen nur die Dummen.

Wichtige Tipps und Tricks zum Kürzen von Brüchen:

1. Lerne die Teilbarkeitsregeln um Brüche schnell zu kürzen.
2. Oft ist es einfacher Schritt für Schritt zu kürzen als auf einmal.
3. Manchmal kannst du für das Kürzen ausklammern.

Ein typischer Fehler besteht darin direkt aus einer Summe zu kürzen. Die folgende Berechnung ist falsch, es darf nicht einfach die 5 aus Zähler und Nenner gestrichen werden.

In diesem Fall sollten Zähler und Nenner ausgerechnet werden.

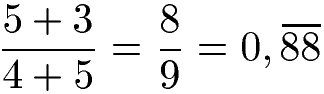
Wie sich zeigt entstehen mit 0,75 und 0,88... zwei verschiedene Quotienten. Daher ist auf die richtige Berechnung zu achten.

Ausklammern und kürzen:

Es gibt durchaus in einigen Fällen die Möglichkeit aus einem Bruch mit Summen oder Differenzen zu kürzen. Dabei muss jedoch ausgeklammert werden, aus der Summe oder Differenz selbst wird hingegen nicht gekürzt. Im nächsten Beispiel zum Kürzen von Brüchen kann die 3 gestrichen werden.

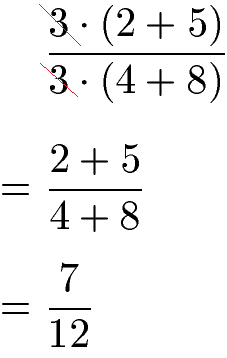
Insbesondere beim Kürzen von Brüchen mit Variablen muss aufgepasst werden. Dazu sehen wir uns nun Beispiele an.

Brüche mit Variablen kürzen

Brüche mit Variablen können gekürzt werden wenn Variablen - oft zusammen mit Zahlen - ausgeklammert werden können. Im nächsten Beispiel wird dabei im Zähler die 2 ausgeklammert. Diese kann nach dem Ausklammern gestrichen werden.

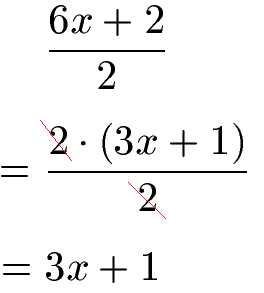
Bei komplizierten Brüchen mit Variablen kann dennoch in manchen Fällen gekürzt werden. Im nächsten Beispiel kann sowohl im Zähler als auch im Nenner 3x ausgeklammert werden. Die 3x können im Anschluss gestrichen (= gekürzt) werden.

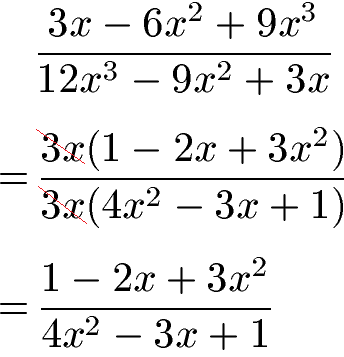
Sehen wir uns nun noch einmal kurz den Unterschied zwischen Brüche kürzen und erweitern an.

Brüche kürzen und erweitern

Brüche kürzen bedeutet den Zähler und den Nenner durch die gleiche natürliche Zahl zu teilen. Dieses teilen kann auch direkt im Bruch passieren, sprich im Zähler und im Nenner.

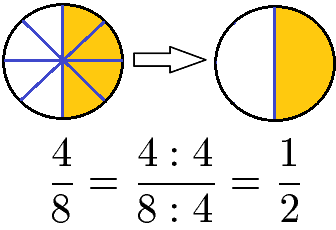
Brüche erweitern bedeutet hingegen den Zähler und den Nenner mit der gleichen natürlichen Zahl zu multiplizieren. Auch diese Multiplikation kann direkt im Zähler und im Nenner stattfinden.

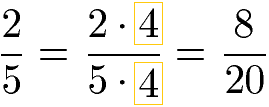
Weitere Links:

• Brüche addieren
• Brüche subtrahieren
• Brüche multiplizieren
• Brüche dividieren
• Zur Mathematik-Übersicht