Brüche zu subtrahieren gehört zu den Grundlagen der Bruchrechnung. Ich zeige dir mit Beispielen wie du gleichnamige und ungleichnamige Brüche subtrahieren kannst. Du lernst wichtige Regeln für die Subtraktion und das Rechnen mit 2 oder 3 Brüchen. Dabei geht es auch um die Subtraktion von ganzen Zahlen und gemischten Brüchen. Die Inhalte liegen als Text und als Video vor.
Brüche helfen dabei Anteile von etwas Ganzem darstellen zu können. Zum Beispiel 3 von 7 Anteilen.
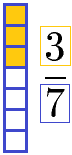
Beim Subtrahieren von Brüchen werden Anteile abgezogen. Um mit Brüchen rechnen zu können, solltest du drei wichtige Begriffe der Bruchrechnung kennen: Zähler, Bruchstrich und Nenner auf. Die Zahl über dem Bruchstrich wird Zähler genannt, die Zahl unter dem Bruchstrich ist der Nenner.

Brüche haben entweder gleiche Nenner oder unterschiedliche Nenner. Die Subtraktion von Brüchen mit gleichen Nennern (= gleichnamige Brüche) ist sehr einfach und dient uns gleich als Einstieg in das Thema. Im Anschluss sehen wir uns den Umgang mit verschiedenen Nennern (= ungleichnamige Brüche) an.
Gleichnamige Brüche subtrahieren
Brüche mit gleichen Nennern werden als gleichnamige Brüche bezeichnet. Sie können sehr einfach subtrahiert werden, indem die Zähler subtrahiert werden und der Nenner beinhalten wird.
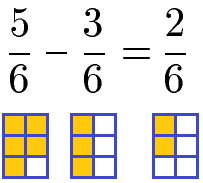
Das Brüche subtrahieren mit gleichnamigen Nennern funktioniert auch wenn Einheiten verwendet werden. Im nächsten Beispiel wird die Längeneinheit Meter verwendet. Die Subtraktion der Brüche findet auch hier durch Subtrahieren der Zähler und Beibehaltung des Nenners statt.
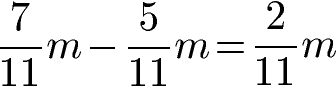
Brüche zu subtrahieren oder zu addieren funktioniert auch mit mehreren Brüchen. Im nächsten Beispiel mit drei Brüchen werden die Zähler addiert bzw. subtrahiert bei gleichem Nenner.
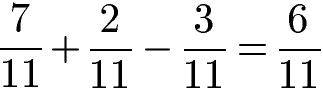
Ist eine Zahl noch unbekannt, wird ein Platzhalter an der Stelle dieser Zahl eingesetzt. In der Grundschule ist das oft ein kleines Rechteck, in welches eine Zahl eingetragen werden muss. Dieser Platzhalter wird später mit einer Variablen (= Buchstaben) ersetzt. Die Subtraktion gleichnamiger Brüche mit Variablen funktioniert im Prinzip so wie wenn nur Zahlen vorkommen.
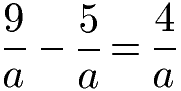
Sofern der Nenner bei allen Brüchen gleich ist, sieht die allgemeine Rechenregel vor, diesen beizubehalten und im Zähler die Zahlen bzw. Variablen zu subtrahieren.
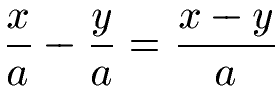
Im nächsten Abschnitt sehen wir uns die Subtraktion ungleichnamiger Brüche an.
Ungleichnamige Brüche subtrahieren
Unter ungleichnamigen Brüchen versteht man Brüche mit unterschiedlichen Nennern. Um ungleichnamige Brüche zu subtrahieren, muss zunächst ein gemeinsamer Nenner für alle Brüche gefunden werden. Es gibt mehrere Wege einen gemeinsamen Nenner bzw. Hauptnenner für alle Brüche zu finden. Starten wir mit einem Beispiel für die einfachste dieser Möglichkeiten.
Wir beginnen damit die beiden Ausgangsnenner miteinander zu multiplizieren.
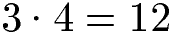
Als gemeinsamer Nenner für beide Brüche wurde die natürliche Zahl 12 berechnet. Um eine 12 in beiden Nennern zu erzeugen, müssen wir die Brüche mit 4 bzw. mit 3 multiplizieren. Dies tun wir sowohl im Zähler als auch im Nenner des Bruchs. Im Anschluss haben wir zwei gleichnamige Brüche mit dem Nenner 12. Bei diesen können wir den Zähler subtrahieren und den Nenner beibehalten.
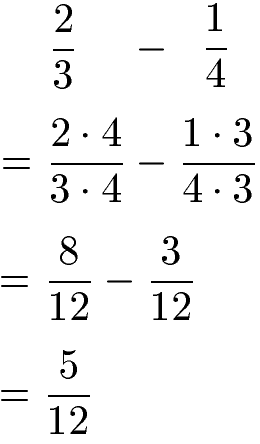
Den Zähler und den Nenner mit der gleichen Zahl zu multiplizieren wird in der Bruchrechnung als Brüche erweitern bezeichnet. Mehr dazu in den nächsten Abschnitten.
Hauptnenner finden mit kgV (kleinstes gemeinsames Vielfaches)
Neben der Multiplikation der beiden Nenner kann ein gemeinsamer Nenner auch mit dem kleinsten gemeinsamen Vielfachen - kurz kgV - berechnet werden. Dieser gemeinsamer Nenner wird Hauptnenner genannt. Für kleine Zahlen lässt sich das kgV mit der Menge der Vielfachen sehr einfach bestimmen. Wir nehmen zunächst noch einmal unser Beispiel von eben:
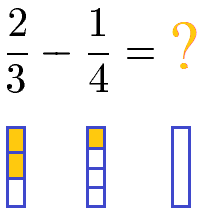
Die Nenner der Brüche sind 3 und 4. Wie bilden die Vielfachen der Zahlen 3 und 4 und schreiben diese in eine Menge.
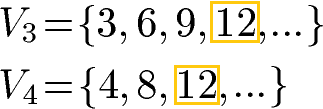
Das kleinste gemeinsame Vielfache - kurz kgV - von 3 und 4 ist die Zahl 12. Die 12 ist damit der gemeinsame Nenner (Hauptnenner). Um auf die Zahl 12 im Nenner zu kommen, muss der erste Bruch mit 4 multipliziert werden. Der zweite Bruch muss mit 3 multipliziert werden. Das Erweitern des Bruchs sieht vor sowohl im Zähler als auch im Nenner mit 4 bzw. 3 zu multiplizieren.
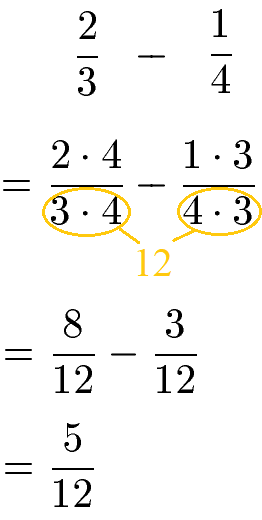
Das kleinste gemeinsame Vielfache für die Nenner der Brüche wurde bisher mit der Multiplikation der Nenner oder der Menge der Vielfachen bestimmt. Für große Zahlen wird jedoch die Primfaktorzerlegung verwendet um das kgV zu berechnen. Dies sehen wir uns als nächstes an.
Mehrere Brüche subtrahieren: Primfaktorzerlegung für kgV
Um einen gemeinsamen Nenner bzw. Hauptnenner von Brüchen mit größeren Zahlen zu finden, wird das kgV mit der Primfaktorzerlegung berechnet. Das nächste Beispiel zeigt die Subtraktion von drei ungleichnamigen Brüchen.
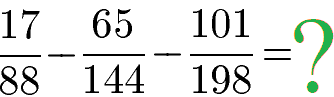
Für jeden Nenner führen wir eine Zerlegung in Primfaktoren durch. Unter der Primfaktorzerlegung versteht man eine Zerlegung einer Zahl in Primzahlen. Die Zerlegung der Zahl 88 ergibt 2 · 2 · 2 · 11. Da die Zahl 2 insgesamt 3 Mal vorkommt wird sie mit der Potenz 23 abgekürzt. Die 11 kommt 1 Mal vor, daher 111.
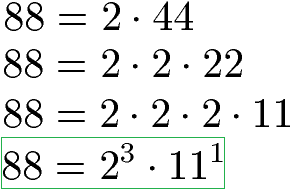
Für die Zahl 144 wird ebenfalls eine Primfaktorzerlegung durchgeführt. Wir erhalten die Zahl 2 insgesamt 4 Mal (= 24) und die Zahl 3 erhalten wir 2 Mal (= 32).
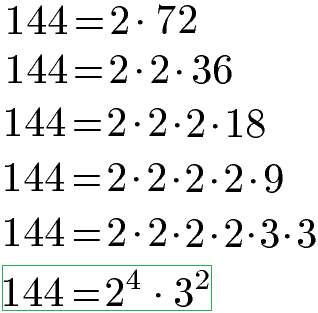
Die Zahl 198 wird ebenfalls in eine Multiplikation aus möglichst kleinen Zahlen zerlegt. Wir erhalten die Zahl 2 insgesamt 1 Mal (= 21), die Zahl 3 erhalten wir 2 Mal (= 32) und die 11 bekommen wir 1 Mal (= 111).
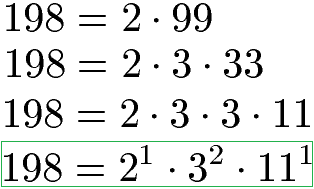
Um das kleinste gemeinsame Vielfache zu berechnen, übernehmen wir die Potenzschreibweise der drei Zahlen. Dabei interessiert uns für alle drei Basen die Potenz mit dem jeweils höchsten Exponenten. Bei der Basis 2 ist dies 24, bei der Basis 3 ist dies 32 und bei der Basis 11 ist dies 111. Die drei ausgewählten Potenzen multiplizieren wir miteinander um das kgV zu berechnen.
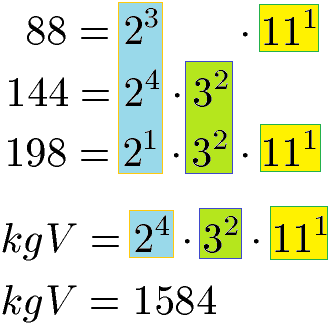
Das kgV der Zahlen 88, 144 und 198 ist 1584. Die 1584 ist unser gemeinsamer Nenner und wir müssen die drei Brüche aus unserer Aufgabenstellung auf 1584 im Nenner erweitern. Um die nötigen Faktoren für die Erweiterung der Brüche zu berechnen, teilen wir diese Zahl durch 88, 144 und 198.
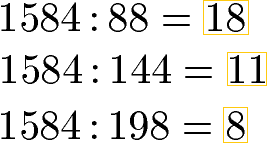
Wir müssen die drei Brüche der Subtraktion mit 18, 11 bzw. 8 erweitern. Zur Erinnerung: Den Bruch erweitern bedeutet sowohl den Zähler als auch den Nenner mit dieser Zahl zu multiplizieren. Wir erhalten drei gleichnamige Brüche mit denen wir dir die Berechnung sehr einfach beenden können.
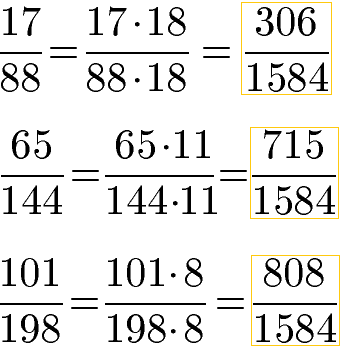
Die drei gleichnamigen Brüche können wir subtrahieren, indem wir die Zähler subtrahieren und den Nenner übernehmen.
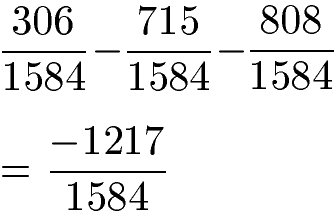
Wir erhalten -1217 : 1584 als Ergebnis.
Brüche subtrahieren: Ganzen Zahlen und negative Zahlen
Um Brüche und ganzen Zahlen zu subtrahieren, wird die ganze Zahl in einen Bruch mit gleichem Nenner umgewandelt. Dabei muss die ganze Zahl mit dem Nenner des Bruchs erweitert werden, sprich Zähler und Nenner des Bruchs werden mit der gleichen Zahl multipliziert. Wir erhalten zwei gleichnamige Brüche und können die Zähler subtrahieren während der Nenner beibehalten wird.
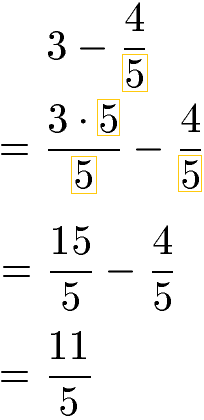
Die Subtraktion von Brüchen funktioniert auch mit negativen Zahlen. In der nächsten Aufgabe wird von der negativen Zahl -4 der Bruch 3 : 8 subtrahiert. Für die Berechnung wandeln wir die -4 in einen Bruch mit gleichem Nenner - in diesem Fall 8 - um. Wir erhalten zwei gleichnamige Brüche und subtrahieren diese im Anschluss.
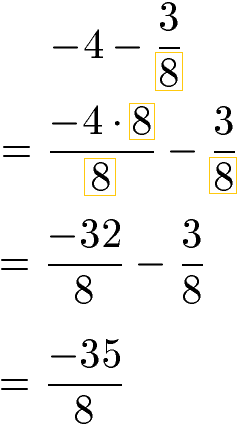
Im nächsten Abschnitt geht es um die Subtraktion von gemischten Zahlen bzw. gemischten Brüchen.
Subtraktion von gemischten Brüchen (gemischten Zahlen)
Um gemischte Brüche bzw. gemischte Zahlen zu subtrahieren, werden die diese in einfache Brüche aus Zähler und Nenner umgewandelt. Als Beispiel zur Subtraktion zweier gemischter Brüche sehen wir uns die folgende Aufgabe an.
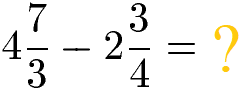
Den ersten Bruch wandeln wir um, indem wie die Zahl (4) auf den Nenner 3 bringen. Dazu erweitern wir den Bruch mit 3, sprich wir multiplizieren Zähler und Nenner mit 3. Wir erhalten zwei gleichnamige Brüche, die wir addieren.
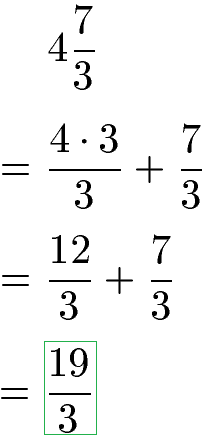
Den zweiten Bruch wandeln wir um, indem wie die ganze Zahl (2) auf den Nenner 4 bringen. Dazu erweitern wir den Bruch mit 4, sprich wir multiplizieren Zähler und Nenner mit 4. Wir erhalten zwei gleichnamige Brüche, die wir addieren.
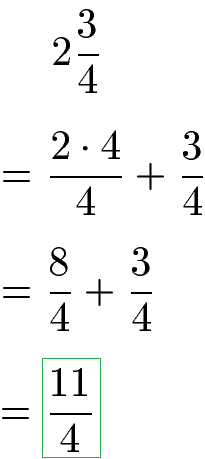
Die zwei gemischten Zahlen haben wir nun in zwei Brüche mit nur Zähler und Nenner umgewandelt. Den gemeinsamen Nenner erhalten wir durch Multiplikation der beiden Nenner mit 4 · 3 = 12. Wir erweitern daher den ersten Bruch mit 4 und den zweiten Bruch mit 3 und können im Anschluss die Subtraktion der Brüche durchführen.
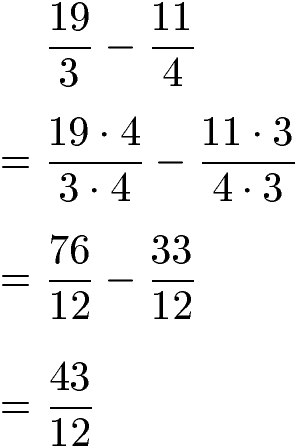
Weitere Empfehlungen:
204 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: