Brüche multiplizieren ▷ Erklärung und Beispiele

Brüche zu multiplizieren und zu kürzen, lernst du in diesem Artikel. Es geht um gemischte Aufgaben aus Multiplikation und Division sowie um ganze Zahlen und gemischte Zahlen. Eine schwierige Aufgabe mit Variablen zeige ich dir am Ende auch. Die Inhalte liegen als Text und als Video vor.

Brüche zu multiplizieren ist grundsätzlich ganz einfach: Zähler mal Zähler und Nenner mal Nenner. Dies zeigt auch ein einfaches Beispiel zur Multiplikation von Brüchen.

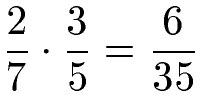
Die Multiplikation von Brüchen bringt jedoch noch weitere Herausforderungen mit sich. Daher solltest du dir die Beispiele und Erklärungen in den nächsten Abschnitten ansehen.

Brüche multiplizieren Beispiele: Bruch mal Bruch

Im Gegensatz zur Addition oder Subtraktion von Brüchen ist es nicht wichtig, ob es gleiche Nenner oder unterschiedliche Nenner bei den Brüchen gibt. Sind die Nenner der beiden Brüche verschieden (= ungleichnamige Brüche) können die Zähler und Nenner dennoch sofort miteinander multipliziert werden.

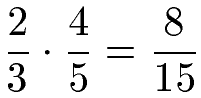
Bei gleichen Nennern (= gleichnamige Brüche) können selbstverständlich auch die Zähler und Nenner jeweils miteinander multipliziert werden.

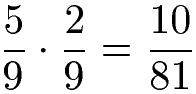
Die Reihenfolge der Brüche spielt bei der Multiplikation keine Rolle. Wie auch beim Kommutativgesetz dürfen die Faktoren vertauscht werden ohne das sich das Produkt ändert.

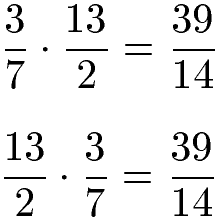
Die Regel zur Multiplikation von Brüchen kann allgemein mit Variablen ausgedrückt werden. Die nächste Gleichung sagt aus, dass beide Zähler und beide Nenner miteinander multipliziert werden.

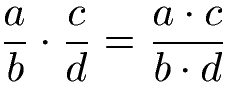
Beim Multiplizieren von Brüchen entstehen sehr schnell Produkte, die gekürzt werden können. Beispiele zum Multiplizieren und Kürzen von Brüchen sehen wir uns jetzt an.

Brüche multiplizieren und kürzen

In vielen Fällen können Brüche multipliziert und im Anschluss gekürzt werden. Kürzen bedeutet den Zähler und den Nenner durch die gleiche Zahl zu teilen. Dies führt dazu, dass der Bruch im Ergebnis kleinere Zahlen aufweist. Im nächsten Beispiel werden zwei Brüche multipliziert und im Anschluss mit 2 gekürzt.

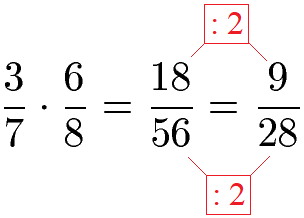
Die Multiplikation von drei Brüchen funktioniert ebenfalls, in dem alle Zähler und alle Nenner miteinander multipliziert werden. Mathematisch richtig ist es die Berechnung von links nach rechts durchzuführen. Es werden erst die beiden linken Brüche miteinander multipliziert und das Ergebnis wird mit dem dritten Bruch mal genommen.

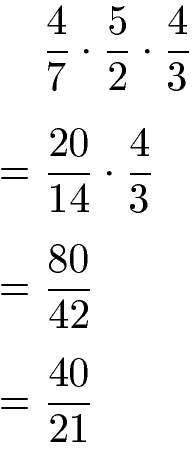
Die Multiplikation der drei Brüche hat das Ergebnis 80 : 42 geliefert. Sowohl 80 als auch 42 können ohne Rest durch 2 geteilt werden und ergeben das gekürzte Ergebnis 40 : 21.

Brüche multiplizieren und dividieren

Das Brüche multiplizieren und dividieren kann auch in einer einzigen Aufgabe vorkommen. Multiplikation und Division sind von der Priorität gleich hoch.

Kommt daher - wie in der nächsten Aufgabe - beides vor, wird die Aufgabe von links nach rechts gerechnet. Zuerst wird die Multiplikation der beiden linken Brüche durchgeführt. Die Division der Brüche wird in eine Multiplikation umgewandelt, indem beim hinteren Bruch Zähler und Nenner vertauscht wird.

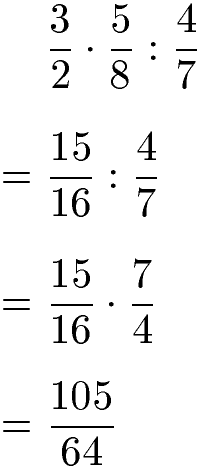
Die Reihenfolge von Division und Multiplikation bei Brüchen kann durch Klammern verändert werden. Im nächsten Beispiel wird daher zuerst die Division der Brüche in der Klammer berechnet. Diese wird durch Vertauschen von Zähler und Nenner beim hinteren Bruch in eine Multiplikation umgewandelt.

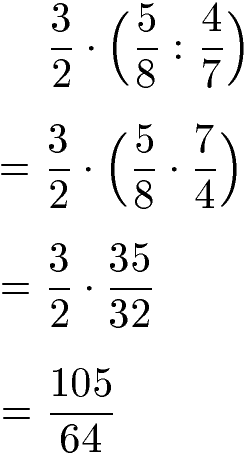
Oft werden Brüche auch mit natürlichen Zahlen oder ganzen Zahlen multipliziert. Sehen wir und dazu einige Beispiele an.

Brüche multiplizieren mit natürlichen Zahlen (ganzen Zahlen)

Brüche können mit natürlichen Zahlen multipliziert werden. Dazu wird die natürliche Zahl mit dem Zähler multipliziert bzw. in den Zähler übernommen.

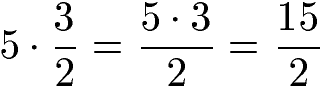
Brüche können mit Zahlen vor oder nach dem Bruch multipliziert werden. Ob es sich dabei um ganze Zahlen, negative Zahlen oder Dezimalzahlen (= Kommazahlen) handelt, spielt dabei keine Rolle.

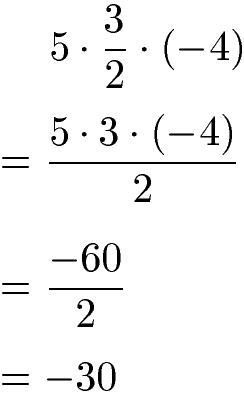
Manchmal sind Zahlen in der Mathematik noch nicht bekannt. In diesem Fall werden Platzhalter verwendet, die in der Mathematik mit Variablen (= Buchstaben) dargestellt werden. Auch hier gilt: Eine Variable vor dem Bruch wird mit dem Zähler multipliziert.

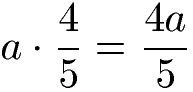
Das nächste Beispiel zeigt wie mit Variablen in Zähler und Nenner umgegangen werden muss.

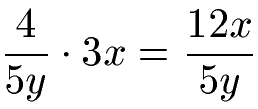
Die Multiplikation von Brüchen kann auch mit gemischten Zahlen bzw. gemischten Brüchen durchgeführt werden. Sehen wir uns dazu einmal Beispiele an.

Bruchrechnung mit gemischten Zahlen

Um zwei gemischte Zahlen bzw. zwei gemischte Brüche miteinander zu multiplizieren, werden die gemischten Zahlen zunächst in Brüche mit nur einem Zähler und Nenner umgewandelt. Als Beispiel dient die Multiplikation zweier gemischter Brüche.

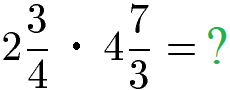
Zunächst wandeln wir den linken gemischten Bruch um. Die ganze Zahl (2) wird dabei mit dem Nenner des Bruchs (4) sowohl im Zähler als auch im Nenner multipliziert. Dies nennt man auch das Erweitern eines Bruchs. Die gleichnamigen Brüche werden addiert.

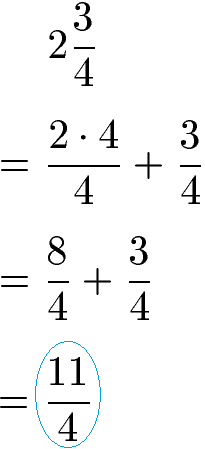
Ebenso wandeln wir den zweiten gemischten Bruch um. Dazu erweitern wir die ganze Zahl (4) mit der 3 vom Nenner. Dies bedeutet, dass wir die 4 mit der 3 multiplizieren und durch 3 teilen. Dadurch erhalten wir einen weiteren Bruch mit nur Zähler und Nenner.

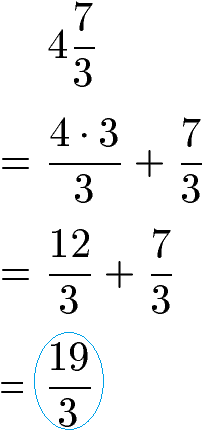
Die beiden Brüche können nun multipliziert werden. Wie immer gilt: Zähler mal Zähler und Nenner mal Nenner.

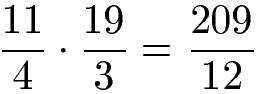
Die Multiplikation der beiden gemischten Brüche ergibt 209 : 12.

Multiplikation bei Doppelbrüchen und Mehrfachbrüchen

Multiplikationen kommen auch bei Doppelbrüchen bzw. Mehrfachbrüchen vor. Im ersten Fall befindet sich im Zähler selbst ein Bruch (a : b), der durch den Nenner (c) geteilt wird. Die allgemeine Schreibweise mit Variablen und ein Beispiel mit Zahlen folgen.

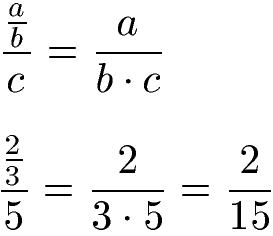
Doppelbrüche bzw. Mehrfachbrüche können auch sowohl im Zähler als auch im Nenner einen Bruch aufweisen. Sehen wir und auch dazu die allgemeine Schreibweise mit Variablen und ein Beispiel an.

Werfen wir einen Blick auf Textaufgaben zu Brüchen.

Textaufgaben (Sachaufgaben) zur Multiplikation

In diesem Abschnitt sehen wir uns einige typischen Textaufgaben bzw. Sachaufgaben zur Multiplikation von Brüchen an.

Beispiel 1: Stimmen bei einer Wahl

Bei einer Wahl wurden 28 Stimmen abgegeben. Marc bekam 8 Stimmen. Bei einer zweiten Wahl konnte er doppelt so viele Stimmen der 28 Personen ergattern. Wie viele Stimmen bekam er im zweiten Wahlgang? Lösung: Er bekam zunächst 8 von 28 stimmen, die verdoppelt werden.

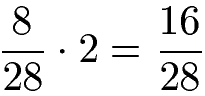
Marc bekam 16 von 28 Stimmen.

Beispiel 2: Fahrrad kaufen

Ein gebrauchtes Fahrrad kostet 240 Euro. Anna hat 5/7 bereits gespart. Wie viel Geld fehlt ihr noch? Lösung: Wir berechnen zunächst wie viel 5/7 von 240 Euro sind. So viel Geld hat sie bereits. Die Differenz zu 240 Euro muss Anna in Zukunft noch sparen.

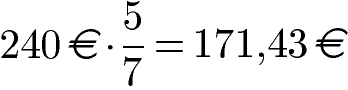
Anna hat 171,43 Euro angespart. Ihr fehlen noch 68,57 Euro um die Kosten vom Fahrrad bezahlen zu können.

Brüche multiplizieren mit Variablen

In diesem Abschnitt soll eine schwere Aufgabe behandelt werden: Das Multiplizieren von Brüchen mit Variablen in den Zählern und Nennern. Folgende Vorgehensweise:

• Zähler mit Zähler multiplizieren, beides in Klammern.
• Nenner mit Nenner multiplizieren, beides in Klammern.
• Terme bzw. Klammern ausmultiplizieren.
• Die Variable x ausklammern und raus kürzen.

Vollständige Rechnung:

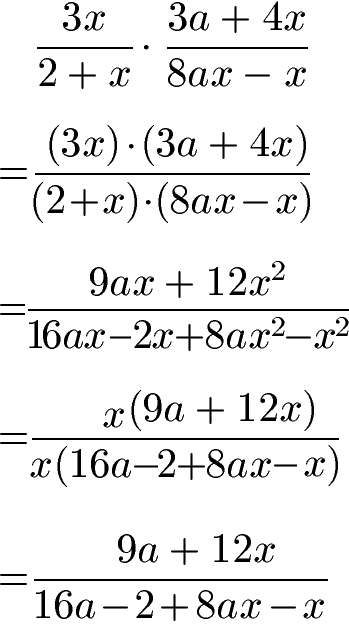
Links:

• Weiter zu: Brüche dividieren
• Weiter zu: Bruchrechnung Übunsaufgaben
• Zurück zu: Bruchrechnung Übersicht
• Zurück zu: Mathematik Übersicht