Schnittwinkel zweier Geraden

Wie man den Schnittwinkel zweier Geraden berechnet, lernt ihr in diesem Artikel der Mathematik. Dazu erhaltet ihr sowohl die allgemeine Formel, als auch ein Rechen-Beispiel.

Bevor wir mit der Berechnung des Schnittwinkels zweier Geraden beginnen, solltet ihr eure Vorkenntnisse kurz checken: Wem die folgenden Themen noch gar nichts sagen, der möge diese bitte erst nachlesen. Alle anderen können gleich mit dem nächsten Absatz weiter machen.

• Ebener Vektor und räumlicher Vektor
• Vektorrechnung: Addition, Subtraktion, Skalarprodukt
• Betrag eines Vektors
• Schnittpunkt zweier Geraden

Schnittwinkel berechnen

Es mag den meisten völlig logisch erscheinen, der Vollständigkeit halber muss man jedoch eine Bedingung für die Berechnung des Schnittwinkels zweier Geraden angeben: Die beiden Geraden müssen sich überhaupt schneiden. Wenn wir zwei Geraden im Raum haben, die sich nirgends schneiden, ist es schwachsinnig, für diese einen Schnittwinkel zu berechnen. Sofern in der Aufgabenstellung nicht explizit angegeben ist, dass sich zwei Geraden schneiden, könnt ihr dies selbst prüfen ( Siehe dazu unser Artikel Schnittpunkt zweier Geraden ).

Ist nun sicher gestellt, dass es einen Schnittpunkt gibt, kann man nun mit der Berechnung des Schnittwinkels beginnen. Dazu als erstes eine kleine Grafik, gefolgt von der Formel zur Berechnung des Winkels:

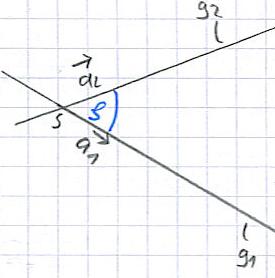
Formel zur Berechnung des Schnittwinkels:

Der Schnittwinkel φ der Geraden g₁ und g₂ mit ihren jeweiligen Richtungsvektoren wird wie folgt berechnet:

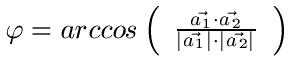
Wichtig: Bevor ihr den arrcos anwendet, solltet ihr den Taschenrechner auf DEG bzw. DEGREE  stellen.

Beispiel:

Im nun Folgenden soll der Schnittwinkel zwischen zwei Geraden berechnet werden. Anmerkung: In unserem Artikel Schnittpunkt zweier Geraden wurde bereits nachgewiesen, dass sich die beiden Geraden überhaupt schneiden.

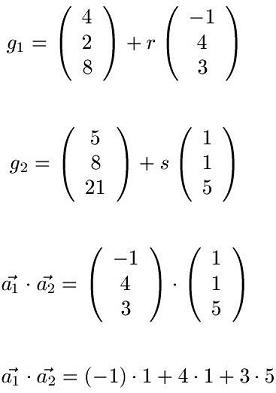
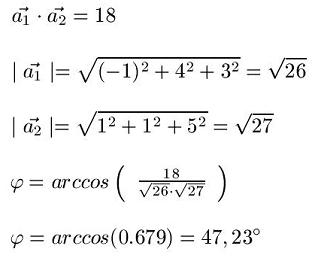
Links:

• Zur Vektor-Übersicht
• Zur Mathematik-Übersicht