Potenzgesetze verstehen ▷ Beispiele

Die Potenzgesetze lernst du in diesem Artikel. Ich zeige dir, wofür du die Potenzgesetze brauchst sowie die Addition, Subtraktion, Multiplikation und Division von Potenzen. Der Umgang mit gleichen und verschiedenen Basen wird mit Beispielen gezeigt. Weiter unten findest du außerdem die Potenzgesetze für Brüche, das Potenzieren von Potenzen, die Potenzregeln für Wurzeln und wie du Potenzen abtrennen kannst.

Die Potenzgesetze dienen dazu Potenzen zu vereinfachen oder umzurechnen. Um die Potenzgesetze - auch Potenzregeln genannt - verwenden zu können, solltest du jedoch einige wichtige Begriffe zu Potenzen kennen. Die wichtigsten Fachbegriffe lauten Basis (= Grundzahl) und Exponent (= Hochzahl). Wird die Potenz ausgerechnet, bezeichnet man das Ergebnis als Potenzwert.

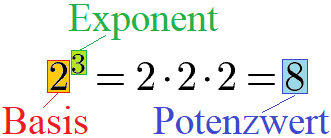
Viele der Potenzgesetze lassen sich nur unter bestimmten Bedingungen anwenden, zum Beispiel muss in beiden Potenzen eine gleiche Basis vorliegen. Achte bei den nun folgenden Gesetzen zu Potenzen darauf, unter welchen Bedingungen diese eingesetzt werden dürfen.

Potenzgesetz der Addition

Bei gleicher Basis und gleichem Exponenten können zwei Potenzen sehr einfach addiert werden: Die Koeffizienten (hier a und b genannt) werden addiert während der restliche Teil unverändert bleibt. Das Potenzgesetz zum Addieren lautet:

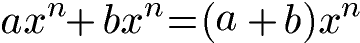
Zwei Beispiele zur Addition von Potenzen sollten dieses doch recht einfache Potenzgesetz verdeutlichen:

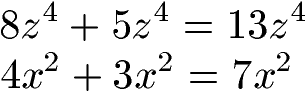
Die Addition von Potenzen mit verschiedenen Basen oder Potenzen kann nicht mit einer Regel allgemein dargestellt werden. In einigen Fällen kann dennoch die Potenz berechnet werden. Wie dies funktioniert und wie du Potenzen mit negativen Zahlen addieren kannst, lernst du unter Potenzen addieren.

Potenzgesetz der Subtraktion

Bei gleicher Basis und gleichem Exponenten können zwei Potenzen sehr einfach subtrahiert werden: Die Koeffizienten (hier a und b genannt) werden subtrahiert während der restliche Teil unverändert bleibt. Das Potenzgesetz zum Subtrahieren lautet:

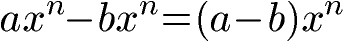
Zwei Beispiele zur Subtraktion von Potenzen sollten dieses doch recht einfache Potenzgesetz verdeutlichen:

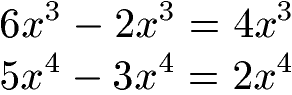
Die Subtraktion von Potenzen mit verschiedenen Basen oder Exponenten kann nicht mit einer allgemeinen Potenzregel gezeigt werden. In einigen Fällen kann dennoch die Potenz berechnet werden. Wie dies funktioniert und wie man die Potenzen mit negativen Zahlen subtrahieren kann, lernst du unter Potenzen subtrahieren.

3 Potenzregeln zur Multiplikation

Zur Multiplikation von Potenzen gibt es 3 Potenzgesetze. Diese unterscheiden das Multiplizieren der Potenzen nach Basis und Exponent.

Gleiche Basis, unterschiedliche Exponenten:

Zwei Potenzen mit gleicher Basis können multipliziert werden, indem die gleiche Basis beibehalten wird und die Exponenten addiert werden. Es folgt die allgemeine Gleichung zur Multiplikation von zwei Potenzen mit gleicher Basis und ein Beispiel.

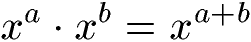
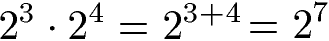
Gleicher Exponent, verschiedene Basen:

Zwei Potenzen mit gleichem Exponenten können multipliziert werden, indem die Basen miteinander multipliziert werden. Der Exponent wird beibehalten: Wichtig: Um die Multiplikation der beiden Basen muss in diesem Fall eine Klammer gesetzt werden. Es folgt die allgemeine Gleichung zur Multiplikation von zwei Potenzen mit gleichem Exponenten und ein Beispiel.

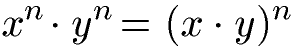
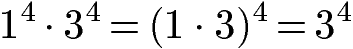
Gleiche Basis, gleicher Exponent:

Potenzen mit gleicher Basis und gleichem Exponenten können multipliziert werden, indem die Basen (innerhalb einer Klammer) multipliziert werden und der gleiche Exponent übernommen wird. Der allgemeine Zusammenhang für die Potenzregel und ein Beispiel lauten:

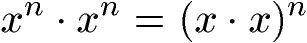
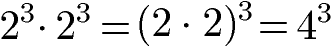
Bei unterschiedlicher Basis und unterschiedlichen Exponenten kann keine allgemeine Gleichung zur Umformung der Potenzen angegeben werden. Weitere Beispiele zu den Potenzgesetzen der Multiplikation und auch zum Umgang mit negativen Zahlen findest du unter Potenzen multiplizieren.

Drei Potenzgesetze zur Division

Die drei Potenzgesetze zur Division dienen dazu beim Dividieren von Potenzen oder bei Brüchen Umformungen zu machen. Zur Erinnerung: Ein Bruch ist nichts anderes als eine Division. Welche der Potenzregeln eingesetzt wird, hängt von den Basen und Hochzahlen der Division bzw. des Bruches ab.

Gleiche Basis, unterschiedlicher Exponent:

Werden zwei Potenzen dividiert bzw. in Form eines Bruchs dargestellt, so kann bei gleicher Basis aber unterschiedlichem Exponenten die Basis übernommen werden und die Exponenten werden subtrahiert. Die allgemeine Gleichung und ein Beispiel folgen.

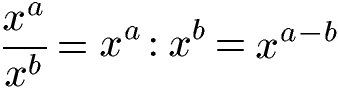
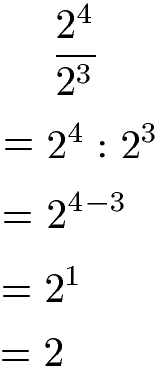
Gleicher Exponent, verschiedene Basen:

Sind bei der Division die Exponenten gleich und die Basis verschieden, können die beiden Basen in einer Klammer zusammen gefasst werden. Der Exponent zu dieser Klammer entspricht dabei der gemeinsamen Basis. Das Potenzgesetz und ein ausgerechnetes Beispiel folgen.

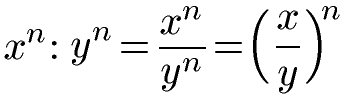
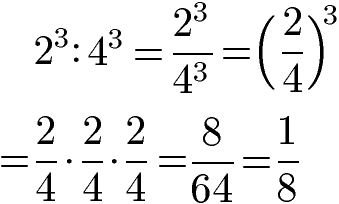
Gleiche Basis, gleicher Exponent:

Bei der Division von zwei Potenzen mit gleicher Basis und gleichem Exponenten ist das Ergebnis 1. Dies ist auch logisch, da der Zähler und der Nenner in der Bruchschreibweise gleich sind und sich gegenseitig vollständig raus kürzen. Die allgemeine Gleichung und ein Beispiel sehen wir uns gleich an.

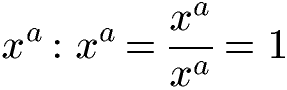
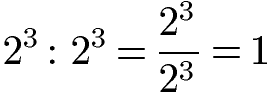
Die Division von Potenzen mit verschiedenen Basen und verschiedenen Exponenten kann nicht mit einem Potenzgesetz angegeben werden. Weitere Beispiele zur Division von Potenzen und auch zum Umgang mit negativen Potenzen findest du unter Potenzen dividieren.

Potenzgesetze für Brüche

Das Potenzgesetz für Brüche dient dazu eine Klammer bei Brüchen zu entfernen oder eine Klammer zu erzeugen. Steht ein Bruch in einer Klammer mit einem Exponenten kann die Klammer entfernt werden. Oder umgekehrt: Zwei Potenzen - eine Potenz im Zähler und eine Potenz im Nenner - kann in eine Schreibweise mit Klammer und Hochzahl umgewandelt werden.

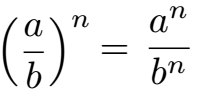
Als Beispiel steht die Division 2 : 3 als Bruch in einer Klammer geschrieben. Diese Klammer selbst ist die Basis einer Potenz mit 4 als Exponenten. Alternativ kann dies auch als Bruch mit zwei Potenzen geschrieben werden.

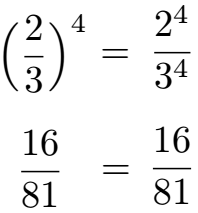
Potenzen potenzieren

Eine Potenz kann selbst die Basis einer anderen Potenz sein. So kann die Potenz aⁿ die Basis sein für eine Potenz mit m als Exponenten. In diesem Fall kann die Potenz vereinfacht werden, indem die Basis a beinhalten wird und die beiden Exponenten miteinander multipliziert werden.

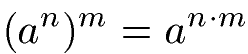
Als Beispiel zum Potenzieren von Potenzen dient die Potenz 5³. Diese steht wiederum in einer Klammer mit einer 2 als Exponenten. Für die Berechnung werden die beiden Exponenten miteinander multipliziert. Im Anschluss kann das Ergebnis berechnet werden.

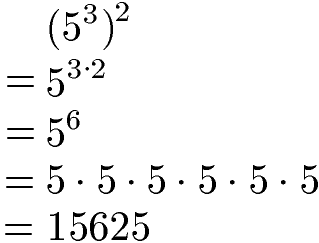
Potenzgesetz bei negativem Exponent

Das Potenzgesetz zum Rechnen mit negativen Exponenten besagt, dass das Vorzeichen des negativen Exponenten umgedreht werden darf indem die Potenz in den Nenner eines Bruchs geschrieben wird. Der Zähler des Bruchs ist dabei 1.

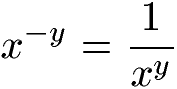
Das Beispiel 3^-4 verfügt über einen negativen Exponenten. Der negative Exponent verschwindet indem die Potenz in den Nenner eines Bruchs geschrieben wird. Beim Exponenten dreht sich dadurch das Vorzeichen um. Der Zähler des Bruchs ist 1. Dieses Beispiel und eine zusätzliche Aufgabe folgen.

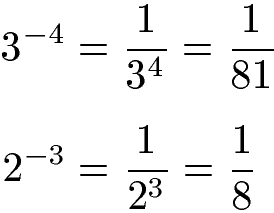
2 Potenzgesetze für Wurzel

Es gibt zwei Potenzgesetze zum Umrechnen von Wurzeln in Potenzen mit Brüchen im Exponenten. Dabei ist eines der Gesetze in dem anderen Gesetz mit beinhaltet. Der Einfachheit halber sollen die beiden Potenzregeln jedoch getrennt betrachtet werden.

Eine Potenz mit einem Bruch im Exponenten kann in eine Wurzel umgewandelt werden. Die Potenz hat dabei die Basis a und im Exponenten 1 geteilt durch n. Dies kann umgeschrieben werden in die n-te Wurzel aus a. Die allgemeine Schreibweise und ein Beispiel folgen.

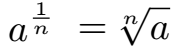
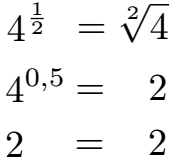
Eine Potenz kann jedoch als Exponenten auch den Quotienten aus zwei Variablen aufweisen. In diesem Fall kann ebenfalls eine Umformung der Potenz in eine Wurzel durchgeführt werden. Auch hierzu die allgemeine Schreibweise und ein Beispiel.

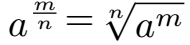
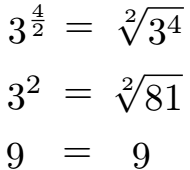
Potenzregeln für abgetrennte Zehnerpotenzen

Potenzregeln helfen auch beim Umgang mit abgetrennten Potenzen bzw. abgetrennten Zehnerpotenzen. Unter einer Zehnerpotenz versteht man eine Potenz mit Basis 10. Diese wird multipliziert mit einem Faktor. Eine solche Schreibweise wird in den Naturwissenschaften und in der Technik dazu verwendet sehr große und sehr kleine Zahlen darzustellen. Zunächst ein Beispiel für große Zahlen:

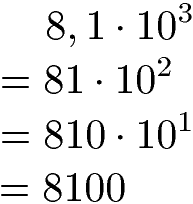
Abgetrennte Zehnerpotenzen können im Exponenten auch eine negative Zahl aufweisen. Bei der Berechnung entsteht dabei eine kleine Dezimalzahl.

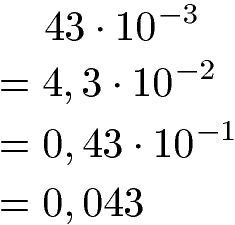
Weitere Erklärungen und Beispiele dazu unter Zehnerpotenzen.