Mit einer Einführung in die Bruchrechnung und entsprechenden Regeln zur Bruchrechnung befassen wir uns in diesem Artikel. Dabei wird zunächst erklärt, worum es denn in der Bruchrechnung überhaupt geht. Im Anschluss sehen wir uns den Umgang mit Brüchen an, also Addition, Subtraktion, Multiplikation und Division von Brüchen. Auch weitere Themen wie Brüche erweitern, Doppelbruch und mehr werden behandelt.
Das Bruchrechnen braucht man dann, wenn es nicht um "ganze" Dinge geht. So isst man oftmals eben nicht eine "ganze" Pizza, sondern nur einen Teil einer Pizza. Nur wie kann man so etwas in der Mathematik ausdrücken? Und genau mit dieser Frage sind wir schon bei einer Einführung in die Bruchrechnung. So kennt jeder sicherlich die Aussage "einen halben Apfel" oder einen "halben Kuchen" essen. Mathematisch würde man das als 1/2 schreiben. Diese Schreibweise nennt man dann einen Bruch. Am Beispiel der Pizza würde dies bedeuten, dass ich die Pizza in 2 Stücke schneide und 1 Stück esse. Würde ich nun sagen, dass ich 3/4 der Pizza esse, bedeutet dies: Ich schneide die Pizza in 4 Stücke und esse 3 Stücke. Die Pizza ist natürlich nur ein aller erstes Beispiel in die Einführung zur Bruchrechnung. Aber jetzt ist es erst einmal wichtig die Schreibweise zu besprechen.
Hinweis: Die Inhalte dieses Artikels liegen auch also Video vor. Siehe hierzu Bruchrechnung Grundlagen Video, Brüche addieren Video, Brüche subtrahieren Video, Brüche multiplizieren Video und Brüche dividieren Video.
Bruchrechnung Einführung: Die Schreibweise
Ein wichtiger Schritt in die Einführung zur Bruchrechnung ist natürlich die Schreibweise. Hier ein paar Beispiele:

Wichtig dabei ist:
- Die Zahl oben ist der Zähler (im Beispiel sind 1, 3, 5, 7 und 8 die Zähler)
- Die Zahl unten ist der Nenner (2, 4, 8, 9 und 10 sind Nenner)
- Dazwischen wird jeweils ein Bruchstrich gezogen
Im Internet werden Brüche oft anders geschrieben: 1/2 oder 3/4. Das hat einen einfachen Grund: Diese Schreibweise ist für die Autoren von Websites oder für Nutzer in Foren deutlich einfacher. Zur besseren Übersicht nutzen wir die aus der Schule "gewohnte" Schreibweise in unseren Artikeln. In den Lösungen der Übungsaufgaben werden jedoch auch wir der Einfachheit halber die andere Schreibweise nutzen. Aber die Lösungen der Aufgaben sollt Ihr ja eh erst ansehen, wenn Ihr die Aufgaben selbst gemacht habt... Noch ein wichtiger Hinweis: Der Bruch 3/4 hat die gleiche Bedeutung wie die von der Division gewohnte Schreibweise: 3 : 4.
Bruchrechnung Regeln: Addition
Esse ich einen halben Kuchen (1/2) und noch einen halben Kuchen (1/2) habe ich insgesamt einen ganzen Kuchen gegessen. Und damit sind wir mitten in der Addition von Brüchen. Es folgen gleich einige Beispiele um die Regeln zur Bruchrechnung zu zeigen, zuvor jedoch kurz die allgemeine Vorgehensweise.
Brüche addieren:
- Brüche auf einen Nenner bringen.
- Den Bruch addieren.
- Kürzen der Brüche.
Schritt 1: Brüche auf einen Nenner bringen
Gehen wir an die Regeln zur Bruchrechnung: Um Brüche addieren zu können, müssen beide den selben Nenner haben. Zur Erinnerung: Der Nenner war das, was "unten" steht beim Bruch. Und der muss - wie eben schon angedeutet - für beide gleich sein. Wichtig dabei ist: Der Wert des Bruches darf sich nicht ändern. Dabei hilft folgendes Wissen: 1 von 2 gleich großen Stücken von einem Kuchen ist gleich viel wie 2 von 4 gleich großen Stücken eines Kuchens. Es folgt ein kleines Beispiel, anhand dessen zwei Möglichkeiten zur Lösung gezeigt werden.
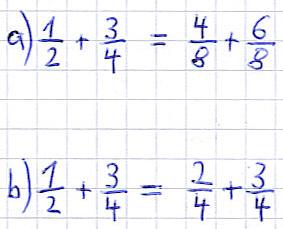
In beiden Fällen soll 1/2 + 3/4 auf einen Nenner gebracht werden. Dabei wurden die beiden eben genannten Möglichkeiten genutzt. Dies funktioniert wird folgt.
Variante a):
- Die beiden Nenner werden miteinander multipliziert. Da 2 · 4 bekanntlich 8 ist, ist der Nenner für die neuen Brüche 8.
- Der Zähler des ersten Bruches wird mit dem Nenner des zweiten Bruches multipliziert. Damit ergibt sich 1 · 4 = 4. Diese 4 ist der neue Zähler des ersten Bruches.
- Der Zähler des zweiten Bruches wird mit dem Nenner des ersten Bruches multipliziert. 2 · 3 = 6. Diese 6 ist der neue Zähler des zweiten Bruches.
Tipp: Lest euch jeden Punkt der Variante a) noch einmal langsam durch und verfolgt diesen anhand des Beispieles a).
Variante b):
- Die 4 des zweiten Nenners ist ein Vielfaches der 2 des ersten Nenners. Um von 2 auf 4 zu kommen, wird mit 2 multipliziert. Also Zähler und Nenner des ersten Bruches mit 2 multiplizieren. Das Ergebnis ist oben zu sehen.
Welche Variante soll ich nutzen?
Die Variante b) ist meist kürzer. Wer sieht, dass die eine Zahl ein Vielfaches der anderen ist, kann diese Variante nutzen. Wem das nicht gelingt, greift am Besten auf Variante a) zurück. Es gibt theoretisch noch eine weitere Möglichkeit unter Einsatz des kleinsten gemeinsamen Vielfachen (Siehe Artikel kgv). Doch dies würde die Sache hier unnötig komplizieren. Wer sich unsicher ist: Variante a) funktioniert immer.
Schritt 2: Den Bruch addieren
Hat man den Bruch erst einmal auf einen Nenner gebracht, ist das Addieren der Brüche ganz einfach. Die beiden folgenden Beispiele zeigen euch, wie dies funktioniert.
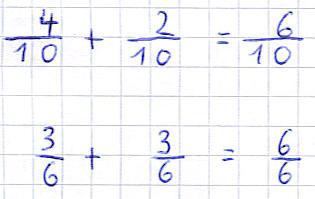
So funktioniert die Addition:
- Die beiden Zähler werden addiert und ergeben den Ergebniszähler.
- Die Nenner sind überall gleich.
Es ist also ganz simpel: Einfach die Zähler addieren und das war es. Der Nenner bleibt.
Schritt 3: Brüche kürzen
Habt Ihr Schritt 1 und Schritt 2 der Addition von Brüchen richtig durchgeführt, solltet ihr auf das richtige Ergebnis gekommen sein. Nun gibt es jedoch oft die Möglichkeit, dieses noch zu vereinfachen. Es folgen erneut Beispiele.

Je kleiner die Zahlen sind, desto einfacher. Deshalb kürzt man die Brüche. Dies funktioniert, wenn Zähler und Nenner durch die gleiche Zahl ohne Rest teilbar sind.
- Beispiel links, oben: Zähler und Nenner des Bruches lassen sich ohne Rest durch 3 teilen.
- Beispiel rechts, oben: Zähler und Nenner des Bruches lassen sich ohne Rest durch 2 teilen.
- Beispiel links, unten: Zähler und Nenner des Bruches lassen sich ohne Rest durch 2 teilen.
- Beispiel rechts, unten: Hier kann nicht mehr gekürzt werden.
Weitere Tipps zum Kürzen:
Beim Kürzen von sehr großen Zahlen ist es oft clever, mehrfach zu kürzen. Sprich den Zähler und Nenner erst mit z.B. mit 2 oder 3 kürzen. Und wenn ihr seht "der Bruch ist auch kürzbar" dann weiterkürzen.
Bruchrechnung Regeln zum Subtrahieren
Zunächst eine kleine Übersicht, was in den meisten Fällen getan werden muss, um Brüche zu subtrahieren:
- Brüche auf einen Nenner bringen
- Brüche subtrahieren
- Ergebnisbruch kürzen
Dies sind die drei Schritte, die bei richtiger Anwendung zum Ergebnis führen. Wir knüpfen uns jeden dieser Punkte nun einzeln vor und erklären, was sich dahinter verbirgt.
Schritt 1: Brüche auf einen Nenner bringen
Um Brüche subtrahieren zu können, müssen beide den selben Nenner haben. Zur Erinnerung: Der Nenner war das, was "unten" steht beim Bruch. Und der muss - wie eben schon angedeutet - für beide gleich sein. Wichtig dabei ist: Der Wert des Bruches darf sich nicht ändern. Dabei hilft folgendes Wissen: 1 von 2 gleich großen Stücken von einem Kuchen ist gleich viel wie 2 von 4 gleich großen Stücken eines Kuchens. Es folgt ein kleines Beispiel, anhand dessen zwei Möglichkeiten zur Lösung gezeigt werden.
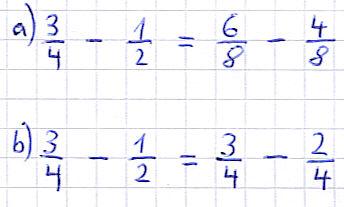
In beiden Fällen soll 1/2 - 3/4 auf einen Nenner gebracht werden. Dabei wurden die beiden eben genannten Möglichkeiten genutzt. Dies funktioniert wie folgt.
Variante a):
- Die beiden Nenner werden miteinander multipliziert. Da 2 · 4 bekanntlich 8 ist, ist der Nenner für die neuen Brüche 8.
- Der Zähler des ersten Bruches wird mit dem Nenner des zweiten Bruches multipliziert. Damit ergibt sich 3 · 2 = 6. Diese 6 ist der neue Zähler des ersten Bruches.
- Der Zähler des zweiten Bruches wird mit dem Nenner des ersten Bruches multipliziert. 1 · 4 = 4. Diese 4 ist der neue Zähler des zweiten Bruches.
Tipp: Lest euch jeden Punkt der Variante a) noch einmal langsam durch und verfolgt diesen anhand des Beispieles a).
Variante b):
- Die 4 des ersten Nenners ist ein Vielfaches der 2 des zweiten Nenners. Um von 2 auf 4 zu kommen, wird mit 2 multipliziert. Also Zähler und Nenner mit 2 multiplizieren. Das Ergebnis ist oben zu sehen.
Welche Variante soll ich nutzen?
Die Variante b) ist meist kürzer. Wer sieht, dass die eine Zahl ein vielfaches der anderen ist, kann diese Variante nutzen. Wem das nicht gelingt, greift am Besten auf Variante a) zurück. Es gibt theoretisch noch eine weitere Möglichkeit unter Einsatz des größten gemeinsamen Teilers. Doch dies würde die Sache hier unnötig komplizieren. Wer sich unsicher ist: Variante a) funktioniert immer.
Schritt 2: Den Bruch subtrahieren
Hat man den Bruch erst einmal auf einen Nenner gebracht, ist das Subtrahieren der Brüche ganz einfach. Die beiden folgenden Beispiele zeigen euch, wie dies funktioniert.
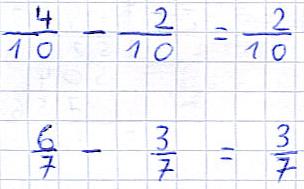
So funktioniert die Subtraktion:
- Die beiden Zähler werden subtrahiert und ergeben den Ergebniszähler.
- Die Nenner sind überall gleich.
Es ist also ganz simpel: Einfach die Zähler subtrahieren und das war es. Der Nenner bleibt. Anmerkung: Sollte der zweite Bruch größer sein als der erste, entsteht wie auch bei der Subtraktion ein negatives Ergebnis. Beispiel: 1/4 - 3/4 = -2/4.
Schritt 3: Brüche kürzen
Funktioniert genauso wie weiter oben unter Brüche addieren Punkt 3.
Bruchrechnung Regeln: Multiplikation
Kommen wir zur Multiplikation von Brüchen.
Die Multiplikation von Brüchen ist wirklich simpel:
- Zähler wird mit Zähler multipliziert.
- Nenner wird mit Nenner multipliziert.
Das war es eigentlich auch schon. Die folgenden Beispiele zeigen euch dies noch einmal:
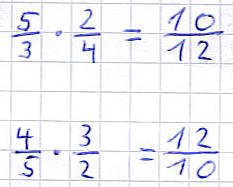
Das war auch schon das ganze Geheimnis hinter der Multiplikation der Brüche: Zähler wird mit Zähler, Nenner wird mit Nenner multipliziert. Noch eine kleine Anmerkung am Rande: Diese Brüche lassen sich natürlich noch kürzen. Der erste Bruch kann auf 5/6 und der zweite auf 6/5 gekürzt werden. Für alle, die mit dem Kürzen noch Probleme haben, empfehle ich den Abschnitt unter Brüche addieren Schritt 3 weiter oben in diesem Artikel.
Bruchrechnung Regeln zur Division
Bleiben noch die Regeln der Bruchrechnung zur Division von Brüchen. Dazu bedient man sich des so genannten Kehrwertes. Dies bedeutet einfach ausgedrückt: Die zweite Zahl wird umgedreht, Zähler und Nenner werden vertauscht. Für alle, die sich das noch nicht ganz vorstellen können, folgt nun ein (komplett durchgerechnetes) Beispiel:

Und so funktioniert die Division von Brüchen:
- Der erste Bruch bleibt wie er ist
- Statt dem ":" wird ein "·" geschrieben
- Der zweite Bruch wird umgedreht, Zähler und Nenner vertauscht
- Die beiden "neuen" Brüche werden multipliziert, wie man das mit Brüchen macht: Zähler · Zähler und Nenner · Nenner.
- Das Ergebnis wird - wenn möglich - gekürzt
Wer noch Probleme beim Kürzen von Brüchen hat findet weiter oben unter Brüche addieren Schritt 3 noch Hilfe hierzu.
Bruchrechnung Regeln: Weitere Themen
Weitere Themen zur Bruchrechnung Einführung und Regeln:
- Brüche kürzen
- Brüche erweitern
- Kehrwert
- Hauptnenner
- Gemischte Zahlen / Gemischte Brüche
- Doppelbruch / Mehrfachbruch/ Mehrere Brüche
- Bruchterme
- Übungsaufgaben mit Lösungen
Links:
117 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: