Die Grundrechenarten der Mathematik lauten Addition, Subtraktion, Multiplikation und Division. Diese vier Grundrechenarten werden ab der Grundschule im Fach Mathematik behandelt. Wichtige Begriffe und Beispiele werden in diesem Artikel vorgestellt. Die Inhalte liegen als Text und als Video vor.
Wir sehen uns gleich die vier Grundrechenarten an. Falls du dich nur für eine bestimmte Grundrechenart interessierst, kannst du auch gleich zu dem entsprechenden Artikel springen:
Die 4 Grundrechenarten:
In den nächsten Abschnitten werden die einzelnen Grundrechenarten behandelt.
1. Grundrechenart: Addition
Die erste Grundrechenart ist die Addition. Man kann hier auch von "hinzufügen" sprechen. Beispiel: Marc hat 2 Äpfel und bekommt weitere 6 Äpfel geschenkt. Er hat nun insgesamt 8 Äpfel.
- 2 + 6 = 8
- Gesprochen: Zwei plus sechs gleich acht.
So etwas kann man auch sehr gut am Zahlenstrahl darstellen. Wir gehen von der 2 um 6 nach rechts und landen auf der 8.
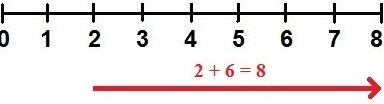
Einige wichtige Begriffe zur Addition solltest man noch kennen. Die erste Zahl vorne wird Summand oder 1. Summand genannt. Nach dem Pluszeichen folgt noch ein Summand, oft auch 2. Summand genannt. Das Ergebnis kommt hinter das Istgleich-Zeichen und wird als Summe bezeichnet.

Es spielt bei der Addition von Zahlen keine Rolle in welcher Reihenfolge die Zahlen stehen. Das Ergebnis ist stets gleich:
- 4 + 5 = 9
- 5 + 4 = 9
- 2 + 3 = 5
- 3 + 2 = 5
Die Addition ist kommutativ, sprich die Reihenfolge der Zahlen darf vertauscht werden. Mehr dazu unter Kommutativgesetz. Weitere Beispiele und Erklärungen zur ersten Grundrechenart findest du unter Addition. Additionen mit großen Zahlen werden oftmals mit der schriftlichen Addition berechnet.
2. Grundrechenart: Subtraktion
Die zweite Grundrechenart ist die Subtraktion. Die Subtraktion ist die Umkehrung der Addition. Anstatt das etwas hinzugefügt wird, zieht man hier etwas ab. Beispiel: Marc hat 8 Äpfel und isst 6 Äpfel auf. Wie viele Äpfel bleiben übrig? Die Antwort lautet 2.
- 8 - 6 = 2
- Gesprochen: Acht minus sechs gleich zwei.
Der nächste Zahlenstrahl zeigt eine Subtraktion. Von der 8 gehen wir um 6 nach links und landen auf der 2.
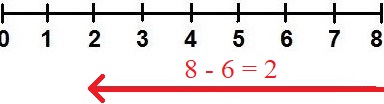
Zur Subtraktion sollte man drei Begriffe kennen. Die erste Zahl wird als Minuend bezeichnet. Nach dem Minuszeichen folgt der Subtrahend. Das Ergebnis hinter dem Gleichzeichen nennt man Differenz.

Im Gegensatz zur Addition spielt die Reihenfolge der Zahlen bei der Subtraktion eine Rolle. Die Subtraktion ist daher nicht kommutativ.
- 5 - 3 = 2
- 3 - 5 = -2
- 8 - 5 = 3
- 5 - 8 = -3
Weitere Erklärungen und Beispiele gibt es unter Subtraktion. Werden die Zahlen größer lohnt sich ein Blick auf die schriftliche Subtraktion.
3. Grundrechenart: Multiplikation
Die Multiplikation ist die dritte Grundrechenart. Die Multiplikation ist eine Abkürzung für die Addition. Zum Lernen der Multiplikation hilft es sich die entsprechende Addition zu verdeutlichen.
Die Multiplikation 2 · 8 = 16 bedeutet, dass die Zahl 8 insgesamt 2 Mal hingeschrieben wird. Dazwischen wird ein Pluszeichen gesetzt. Dies ergibt ebenfalls 16.
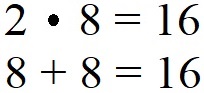
Die Multiplikation 3 · 4 = 12 bedeutet, dass die Zahl 4 insgesamt 3 Mal hingeschrieben wird. Dazwischen wird ein Pluszeichen gesetzt. Dies ergibt ebenfalls 12.
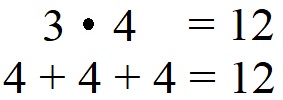
Wie auch bei der Addition darf bei der Multiplikation die Reihenfolge der Zahlen vertauscht werden:
- 3 · 4 = 12
- 4 · 3 = 12
- 5 · 2 = 10
- 2 · 5 = 10
Die Multiplikation ist kommutativ, sprich die Reihenfolge der Zahlen darf vertauscht werden. Mehr dazu unter Kommutativgesetz. Weitere Beispiele und Erklärungen zur dritten Grundrechenart findest du unter Multiplikation. Multiplikationen mit großen Zahlen werden oftmals mit der schriftlichen Multiplikation berechnet.
4. Grundrechenart: Division
Die vierte Grundrechenart ist die Division. Die Division ist die Umkehrung der Multiplikation. Dividieren oder Division bedeutet nichts anderes als verteilen. Die nächste Grafik zeigt wie 6 grüne Bälle auf 2 Körbe gleichmäßig verteilt werden. Dies bedeutet, dass in jedem Korb 3 grüne Bälle landen.
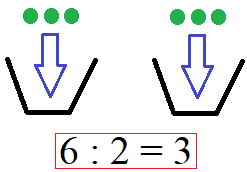
Werden 6 grüne Bälle auf 2 Körbe verteilt wird daraus die Rechenaufgabe:
- 6 : 2 = 3
- Gesprochen: Sechs durch zwei gleich drei.
Um die Division zu lernen, hilft es, sich die entsprechende Multiplikation klar zu machen.
Beispiele Division:
- 18 : 6 = 3, denn 3 · 6 = 18
- 15 : 5 = 3, denn 3 · 5 = 15
- 24 : 6 = 4, denn 4 · 6 = 24
Größere Zahlen werden mit der schriftlichen Division berechnet.
Punkt vor Strich:
Wird mit mehreren Zahlen in einer Aufgabe gerechnet sollte die Regel Punkt vor Strich beachtet werden. Ebenfalls wichtig: Bei großen Zahlen wird schriftliches Rechnen eingesetzt.
Grundrechenarten schriftlich:
- Punkt vor Strich
- Schriftliche Addition
- Schriftliche Subtraktion
- Schriftliche Multiplikation
- Schriftliche Division
- Mathematik Übersicht
277 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: